이번 시간에는 다익스트라 알고리즘의 동작 원리를 살펴보겠습니다.
다익스트라 알고리즘(Dijkstra Algorithm) - "둘러보면서 작은 값으로 바꾸자"
- 그래프의 출발점에서부터 각각 최단 경로를 찾는 알고리즘 입니다.
- 가장 좋아보이는 것부터 찾아가므로 그리디 알고리즘에 해당합니다.

위의 그래프에 데이크스트라 알고리즘을 적용할 것입니다. 초반에는 노드 값(S에서 *까지의 거리)을 모두 ∞로 둡니다.
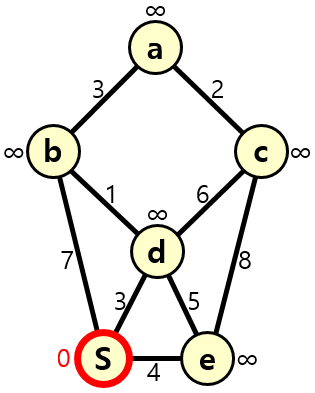
우선 시작점인 S에 포커스를 둡니다

포커스에서부터 주위를 둘러보면서 값을 비교할 것입니다. 만약 '포커스된 노드 값 + 간선 값' 이 '발견된 노드 값' 보다 더 작으면 더 작은 값(더한 값)으로 대체합니다. 위의 사진의 경우 아래와 같습니다.
포커스된 노드 (S) : 0
간선 (S-e) : 4
발견된 노드 (e) : ∞
∴ '포커스된 노드 값 + 간선 값 (4) < 발견된 노드 값 (∞)' 이 성립하므로 대체합니다.

포커스된 노드 (S) : 0
간선 (S-d) : 3
발견된 노드 (d) : ∞
∴ '포커스된 노드 값 + 간선 값 (3) < 발견된 노드 값 (∞)' 이 성립하므로 대체합니다.

포커스된 노드 (S) : 0
간선 (S-b) : 7
발견된 노드 (b) : ∞
∴ '포커스된 노드 값 + 간선 값 (7) < 발견된 노드 값 (∞)' 이 성립하므로 대체합니다.

둘러보기를 끝낸 S를 무효화시키고 e로 포커스를 옮깁니다. S는 무효 처리 되었으므로 수색에서 제외됩니다.

포커스된 노드 (e) : 4
간선 (e-c) : 8
발견된 노드 (c) : ∞
∴ '포커스된 노드 값 + 간선 값 (12) < 발견된 노드 값 (∞)' 이 성립하므로 대체합니다.

포커스된 노드 (e) : 4
간선 (e-d) : 5
발견된 노드 (d) : 3
∴ '포커스된 노드 값 + 간선 값 (9) < 발견된 노드 값 (3)' 이 성립하지 않으므로 대체하지 않습니다.

S는 수색에서 제외되었으므로 접근하지 않고 건너뜁니다.

둘러보기를 끝낸 e를 무효화시키고 d로 포커스를 옮깁니다.

포커스된 노드 (d) : 3
간선 (d-c) : 6
발견된 노드 (c) : 12
∴ '포커스된 노드 값 + 간선 값 (9) < 발견된 노드 값 (12)' 이 성립하므로 대체합니다.

포커스된 노드 (d) : 3
간선 (d-b) : 1
발견된 노드 (b) : 7
∴ '포커스된 노드 값 + 간선 값 (4) < 발견된 노드 값 (7)' 이 성립하므로 대체합니다.

둘러보기를 끝낸 d를 무효화시키고 b로 포커스를 옮깁니다.

포커스된 노드 (b) : 4
간선 (b-a) : 3
발견된 노드 (b) : ∞
∴ '포커스된 노드 값 + 간선 값 (7) < 발견된 노드 값 (∞)' 이 성립하므로 대체합니다.

둘러보기를 끝낸 b를 무효화시키고 c로 포커스를 옮깁니다.

포커스된 노드 (c) : 9
간선 (c-a) : 2
발견된 노드 (a) : 7
∴ '포커스된 노드 값 + 간선 값 (11) < 발견된 노드 값 (7)' 이 성립하지 않으므로 대체하지 않습니다.

둘러보기를 끝낸 c를 무효화시키고 a로 포커스를 옮깁니다.

그러나 a 주변의 모든 노드가 다 무효화 되었으므로 수색을 진행하지 않습니다. 이렇게 모든 노드가 다 무효화 되었으므로 모든 작업을 종료합니다.

각 노드의 최소 비용을 계산하였습니다!

선을 그으면 위와 같습니다 ^^
<출처>
위키백과: 데이크스트라 알고리즘
'IT강의 > 알고리즘' 카테고리의 다른 글
| 연결 리스트의 종류 (0) | 2021.07.28 |
|---|---|
| 스택과 큐의 차이 (0) | 2021.07.28 |
| 크루스칼 알고리즘 (1) - 동작 원리 (0) | 2021.07.28 |
| DFS와 BFS의 차이 (0) | 2021.07.20 |
| 2018년도 정보처리기사 실기 2회 문제풀이 및 해설 - 1. 순서도 (0) | 2020.12.27 |